Fan Maowei' Blog

微信抢红包算法实现（Python）

算法 抢红包
字数统计: 4.1k阅读时长: 18 min
2020/01/25 Share

💬 写在最前

  首先，新的一年，祝大家2020鼠年新春快乐啊！

  同时，也希望武汉加油，中国加油，祝大家都能平平安安，健健康康。


图片均来自网络

(友情提醒，本文除此博客外，作者未在其他平台发布。如要引用，请先与本人取得联系，谢谢理解。)


❔ 问题提出

  新春虽然快乐，但我却有了迷惑。

  什么迷惑呢？

  相信大家这几天都会发红包，也会抢红包。可是，大家有想过，为什么自己就抢得这么少呢?(不会就我一人脸黑吧[手动狗头])

  当然，这不是全部重点，重点还有，为什么抢到的有些红包这么吉利呢？(虽然少)

  比如，20元的红包，有人就会抢到 1.66元，0.88元，等诸如此类”幸运”的数字。

  然后，我就开始好奇，微信抢红包的算法究竟是怎样实现的?（程序员上线）


🔍 开始思考

  首先，假如一次红包是100元(为了便于计算和理解)，然后红包个数是10个(只发一个就毫无必要计算了，抢就完事儿)，每次最小限额是0.01分(按照微信标准)

  有人会想，抢红包，不就 每个人获得剩余红包的一个随机数额 不就好了吗？(但注意要保证最后一个抢的人至少还有1分钱可以领)

  打比方，第一个抢红包的人领取的红包数额是0~100元之间的一个随机数额

  第二个抢红包的人领取的红包数额是0~剩余数额(减去前面的人抢完之后) 之间的一个随机数额

  依次往下，直到最后一个人抢完。

  但这个时候”手残党”们可能会有意见了，其中会有聪明的人提出质疑：这个方法，只对那些 优先 抢红包的人有利，因为抢得越快，获得高金额红包的概率就越大！

  真是这么回事吗？

  其实不难发现，对于上述假设，10人平分100元红包，平均每个人能抢到10元钱。而如果采取刚刚那个算法，第一个抢的人则是从0~100的数额之间随机抢到一个大小，那么他能抢到的平均红包数额是50元！后面的人依次红包数额减小。所以，这个算法，仅对优先抢的人有利。正所谓，早起的鸟儿有虫吃，手速快的人，有钱领。

  （稍微解释一下，我们这里所说的，只是优先抢的人，抢到高额红包的 概率 更大！并不是优先抢的人 一定 比后面抢的人红包更大）

  咳咳，可是，我们平时用微信抢红包真是这样的吗？

  通过大家抢红包这么多年的经验看，好像微信抢红包对每一个人都是相对公平的吧？似乎没有区分过先来后到。

  那么咱是不是就得考虑考虑其他算法了？不过，这个算法难道就不可行吗？我凭单身这么多年的手速，我多抢点钱不好吗？

  所以，咱们就还是把这个算法用Python实现一下，至少它在某些方面是有可行之处的：


💡 编程解决

  • 手速快，拿钱概率高 算法：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    # Python 内置随机数模块
    import random

    # 定义一个问题类
    class Q(object):
        # 初始化
        def __init__(self, money=100.0, amount=10):
            # 红包大小
            self.money = money
            # 红包数量
            self.amount = 10
            # 抢红包的人，人数等于红包数量
            self.people = [0.0] * amount

        # 计算
        def out(self):
            '''
            由于微信最小金额设置是0.01元，
            为方便计算，我们红包数据先统一乘以 100
            目的是将可能出现的小数转换为整数。
            最后计算完成，再在原来数据上统一除以 100
            '''
            self.money *= 100
            # 循环遍历每个人(开始抢)，但不包括最后一个人
            for i in range(self.amount-1):
                # 为了保证后面每一个人至少还能领0.01元(*100=1)
                while True:
                    # 模拟 do~while 语法
                    self.people[i] = random.randrange(1, self.money, 1)
                    if self.money-self.people[i] >= self.amount-1-i:
                        self.money -= self.people[i]
                        break
                # 还原数据
                self.people[i] /= 100

            # 剩余的钱都是最后一个人的
            self.people[-1] = self.money / 100
            # 输出
            print(self.people)

    if __name__ == "__main__":
        q = Q(money=100.00, amount=10)
        q.out()

  • 我们模拟20次输出（红包大小：100元，红包数量：10个），能发现，红包最后几个抢的人，是真的惨！（有兴趣的小伙伴，可以用这个代码多实现几次模拟数据，用于一些统计需求）


表格数据
1 2 3 4 5 6 7 8 9 10
1. 79.93 9.63 4.65 2.54 0.47 0.93 0.64 0.41 0.01 0.79
2. 9.45 89.06 1.13 0.04 0.2 0.04 0.02 0.04 0.01 0.01
3. 23.85 67.55 2.06 5.61 0.52 0.34 0.03 0.01 0.02 0.01
4. 80.07 0.57 16.13 1.72 1.43 0.02 0.02 0.01 0.02 0.01
5. 39.29 0.18 13.05 46.24 0.68 0.18 0.22 0.03 0.04 0.09
6. 71.5 17.01 8.53 0.75 1.77 0.36 0.05 0.01 0.01 0.01
7. 48.0 1.47 9.7 1.92 10.15 27.14 0.49 0.35 0.74 0.04
8. 56.67 0.54 5.08 24.82 4.3 6.51 0.83 1.06 0.05 0.14
9. 64.13 2.65 19.91 9.6 0.41 1.36 1.82 0.04 0.03 0.05
10. 81.75 6.85 8.45 0.29 0.46 1.06 0.99 0.02 0.12 0.01
11. 61.24 12.78 12.44 8.22 3.6 0.88 0.04 0.44 0.11 0.25
12. 42.43 5.23 14.21 26.55 6.64 3.87 0.93 0.1 0.02 0.02
13. 18.14 49.41 10.03 13.62 0.62 4.89 1.67 0.71 0.35 0.56
14. 61.72 0.23 24.47 4.32 7.97 0.46 0.32 0.44 0.04 0.03
15. 21.97 8.93 6.02 23.73 1.77 4.55 1.08 1.71 3.65 26.59
16. 84.32 5.34 5.62 0.55 2.2 0.73 0.34 0.79 0.05 0.06
17. 4.93 35.89 48.15 5.01 5.41 0.26 0.24 0.08 0.01 0.02
18. 95.78 1.98 1.89 0.06 0.12 0.06 0.06 0.01 0.01 0.03
19. 0.53 32.19 31.53 3.17 7.36 23.21 1.63 0.31 0.05 0.02
20. 54.4 21.27 17.67 6.58 0.03 0.01 0.01 0.01 0.01 0.01
平均 50.005 18.438 13.036 9.267 2.806 3.843 0.572 0.329 0.267 1.438


  现在我要模拟微信抢红包实现方式，即，咱不靠手速，纯靠运气，可以不。（可以是可以，不过我想插一句，如果红包个数一共就那么多个，因为你手速慢，而别人抢完了，何不多练练自己手速？）


如何才能公平？

  我们思考这个问题，可以把100元拟作成一条直线，10个人可以拟作成直线上不重合的9个点。即，我们可以在直线上随机取9个不重合的点，把直线随机分成10段，抢红包的人可以依次“获得”直线的每一段，直线的长度就是我们抢到的红包大小！

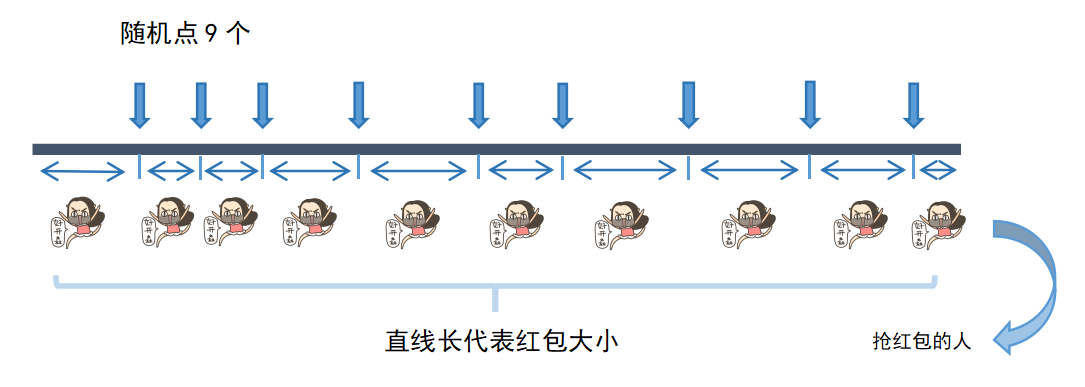
  特别说明：本“抢红包算法”只是作者提出的一种可行思路，并不代表微信实际开发团队使用如此。微信开发团队使用的是什么算法我也不知道=.=

编程实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
# Python 内置随机数模块
import random

# 定义一个问题类
class Q(object):
    # 初始化
    def __init__(self, money=100.0, amount=10):
        # 红包大小
        self.money = money
        # 红包数量
        self.amount = 10
        # 结点数，等于红包数量-1
        self.node = [0] * (amount - 1)
        # 抢红包的人，人数等于红包数量
        self.people = [0.0] * amount

    # 计算
    def out(self):
        '''
        由于微信最小金额设置是0.01元，
        为方便计算，我们红包数据先统一乘以 100
        目的是将可能出现的小数转换为整数。
        最后计算完成，再在原来数据上统一除以 100
        '''
        self.money *= 100
        for i in range(self.amount-1):
            while True:
                # 模拟 do~while 语法
                n = random.randrange(1, self.money, 1)
                if n not in self.node:
                    # 新生成的随机结点不在 node 列表中则满足
                    self.node[i] = n
                    break
        
        # 对结点进行升序排序
        self.node.sort()
        # 根据结点间长度生成每人红包大小
        self.people[0] = self.node[0] / 100
        self.people[-1] = (self.money - self.node[-1]) / 100
        for i in range(1, self.amount-1):
            self.people[i] = (self.node[i] - self.node[i-1]) / 100

        # 输出
        print(self.people)

if __name__ == "__main__":
    q = Q(money=100.00, amount=10)
    q.out()

模拟输出分析

1 2 3 4 5 6 7 8 9 10
1. 4.2 4.3 0.2 32.06 6.54 26.6 8.13 15.15 2.04 0.78
2. 20.63 17.94 2.87 7.44 3.97 4.04 2.61 9.4 5.15 25.95
3. 20.07 4.17 21.27 2.75 7.03 7.43 19.61 2.82 11.13 3.72
4. 8.55 12.49 11.0 8.9 20.6 3.65 0.27 16.04 9.22 9.28
5. 10.16 11.84 5.37 5.38 3.75 2.45 19.53 10.6 20.97 9.95
6. 25.76 14.73 4.44 3.78 4.61 8.38 0.69 2.71 21.19 13.71
7. 1.48 31.14 2.96 2.01 13.08 14.28 5.87 9.94 13.67 5.57
8. 7.21 22.63 0.64 6.81 20.79 9.2 6.43 4.44 17.44 4.41
9. 9.36 3.17 35.82 1.17 12.51 15.12 8.13 4.46 2.59 7.67
10. 5.1 5.28 1.92 8.2 8.96 10.21 32.12 1.58 26.36 0.27
11. 3.1 2.72 1.48 45.51 1.9 4.2 19.38 11.33 8.39 1.99
12. 4.09 2.22 9.43 2.11 31.25 2.06 6.41 5.79 32.19 4.45
13. 14.04 11.56 2.83 4.45 6.54 6.5 5.77 5.85 21.27 21.19
14. 2.57 0.61 32.13 8.6 12.36 8.33 7.89 11.98 10.88 4.65
15. 12.64 15.44 1.28 0.15 3.18 23.68 17.97 9.65 3.43 12.58
16. 5.5 11.73 16.35 0.47 10.99 13.77 6.28 26.55 4.47 3.89
17. 9.21 0.87 0.53 5.93 12.25 8.33 12.44 0.83 44.65 4.96
18. 5.81 4.78 19.94 8.17 2.26 0.64 15.44 0.36 7.98 34.62
19. 8.32 17.92 4.21 5.09 0.99 3.18 12.76 17.56 27.33 2.64
20. 28.29 2.91 2.25 23.93 10.0 22.27 0.16 3.63 0.36 6.2
平均 10.304 9.923 8.846 9.146 9.678 9.716 10.394 8.534 14.535 8.924

可以看到，只要样本数量足够大，每个人平均都能获得10元钱。即不分先后，抢到红包的人运气都“一样”


💸 程序优化

  通过上述算法，我们的确实现了 对于每个抢到红包的人，不分先后的获得了一个随机红包大小。但是，我们还没有实现红包数额的 “吉利化”。

  （其实通过样本数据我们能看到，每一次红包分配出的金额里，都会有几个相对吉利的数字。吉不吉利主要也是看人们的心态，虽然我并不知道微信抢红包算法是如何实现，但是我觉得此算法已经可以使用）

  ——“所以你就不想实现红包数额的‘吉利化’了吗？你就想偷懒了吗？”

  ——“不不不，纵使我觉得上述算法已经可以，但是大过年的，我还是希望每个抢到红包的人都能获得一个相对吉利的红包数额！”

如何取得更多的吉利数字？

  像，6、8、9，包括1（幺，等同于“要”）这样的数字，是大家普遍比较喜爱的。我们要让这些数字尽可能多的出现在我们抢到的红包数额中。

  这里有两种考虑模式：1.“被动”选择、2.“主动”选择

1. “被动”选择

  何为“被动”选择？即我们按照上述第二种算法，照常算出一组结果（用列表或数组存储）。再对每个人抢到的红包数额做分析，如果出现 吉利数 的频次符合我们的预期，则保留我们这组结果，否则，重新获取一组新的结果。循环直到满足退出。

  注意： 这样的编程逻辑虽然很简单，但是要使用到我们的 do~while 直到型循环，而 Python 中并不提供这样的原生语法，所以我们只能通过语法逻辑，自己构建。

  这样的算法模式，优点是，不需要我们去做大量的前期数据处理工作，用大量的随机结果去满足我们需要的条件。很明显，对比于后面我们要讲的“主动”选择，会提高大量的时间复杂度！

  下面就结合上述第二例代码来实现一下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
# Python 内置随机数模块
import random

# 定义一个幸运数类
class Lucky(object):
    # 初始化
    def __init__(self, lucky_numbers=[]):
        # 默认 1,6,8,9 是幸运数
        self.lucky_numbers = [1, 6, 8, 9]
        # 用户可以提供其他幸运数
        self.lucky_numbers += lucky_numbers
        # 消去重复元素，先取其集合，再取其列表
        self.lucky_numbers = list(set(self.lucky_numbers))

    # 是否是幸运数
    def is_lucky(self, number):
        # 使用仿三元表达式 ?:
        return True if number in self.lucky_numbers else False

# 定义一个问题类
class Q(object):
    # 初始化
    def __init__(self, money=100.0, amount=10):
        # 红包大小
        self.money = money
        # 红包数量
        self.amount = 10
        # 结点数，等于红包数量-1
        self.node = [0] * (amount - 1)
        # 抢红包的人，人数等于红包数量
        self.people = [0.0] * amount

    # 计算
    def out(self):
        '''
        由于微信最小金额设置是0.01元，
        为方便计算，我们红包数据先统一乘以 100
        目的是将可能出现的小数转换为整数。
        最后计算完成，再在原来数据上统一除以 100
        '''
        self.money *= 100
        for i in range(self.amount-1):
            while True:
                # 模拟 do~while 语法
                n = random.randrange(1, self.money, 1)
                if n not in self.node:
                    # 新生成的随机结点不在 node 列表中则满足
                    self.node[i] = n
                    break

        # 对结点进行升序排序
        self.node.sort()
        # 根据结点间长度生成每人红包大小
        self.people[0] = self.node[0] / 100
        self.people[-1] = (self.money - self.node[-1]) / 100
        for i in range(1, self.amount-1):
            self.people[i] = (self.node[i] - self.node[i-1]) / 100

        # 输出
        return self.people


if __name__ == "__main__":
    # 实例化 Lucky 类
    l = Lucky()
    # 预期达到频次
    freq = 0.5
    # 红包结果
    results = []

    # 模拟 do~while 语法
    while True:
        # 满足幸运数个数
        count = 0
        # 数字总数
        total = 0
        # 实例化 Q 类
        q = Q(money=100.00, amount=10)
        results = q.out()

        # 取得每个人红包数额
        for r in results:
            # 对红包数额字符串化(乘以100消去小数点)
            string = str(int(r*100))
            # 取得字符串中每个字符
            for char in string:
                # 字符转数字
                num = int(char)
                if l.is_lucky(num):
                    count += 1
                total += 1

        # 满足频次则退出
        if count / total > freq:
            break

    # 输出
    print(results)

2. “主动”选择

  何为“主动”选择？相比于“被动”选择，我们只做完备的前期数据处理，一次结果输出，即满足我们的结果。而不需要“被动”选择中用 直到型循环 去试结果。

  可是，前期数据处理？这就难办了…

  首先，如果发的红包数额相对较大，别人抢到大红包（大于10元）的概率也就越大。我们这里先做一个 “约定”：抢到10元以上红包的人，就不考虑将其数字吉利化了，因为抢到10元红包以上的人，我相信不会特别在乎是不是10.66元或者18.88元，从金额上说，他们大概率也都满足了，所以我们只对那些只抢到10元以下红包的人做数字吉利化。（这也是为了方便行事，说白也算是一种偷懒=。=）

  所以，这个问题就被我们 简(tou) 化(lan) 成：对抢到的10元以下红包，多加入1、6、8、9这样的数字（如 0.66、0.68、0.88、1.68、1.99……）

  现在，我就先把这个思路留在这儿，供读者们自己去解决了！


  感谢阅读！




原文作者：范茂伟

原文链接：http://fmw666.github.io/2020-01-25/微信抢红包算法实现/

发表日期：January 25th 2020, 12:00:00 am

更新日期：February 16th 2020, 7:22:09 pm

版权声明：本文采用知识共享署名-非商业性使用 4.0 国际许可协议进行许可

CATALOG
  1. 1. 💬 写在最前
  2. 2. ❔ 问题提出
  3. 3. 🔍 开始思考
  4. 4. 💡 编程解决
    1. 4.1. 如何才能公平？
    2. 4.2. 编程实现
    3. 4.3. 模拟输出分析
  5. 5. 💸 程序优化
    1. 5.1. 如何取得更多的吉利数字？
      1. 5.1.1. 1. “被动”选择
      2. 5.1.2. 2. “主动”选择
Total : 5
2020
2018
git 后台 算法 抢红包 C语言 游戏 命名 递归
IT